Résolution de système de trois équations linéaires à trois inconnues
Système de trois équations linéaires
a
11x
1 + a
12x
2 + a
13x
3 = b
1
a
21x
1 + a
22x
2 + a
23x
3 = b
2
a
31x
1 + a
32x
2 + a
33x
3 = b
3
où x
1, x
2 и x
3sont inconnues
a
11,..., a
33 sont les coefficients du système
b
1, b
2 и b
3 sont les second membres
Pour résoudre le système de trois équations à trois inconnues 3x3 à l'aide de la calculatrice, entrez les facteurs pertinents, et appuyez sur "Résoudre". Vous pouvez entrer des nombres entiers, les fractions et les décimales.
Comments résoudre un système de 3 équations à 3 inconnues par la règle de Cramer
Règle de Cramer pour la résolution de systèmes linéaires quadratiques des équations algébriques dont le principal déterminant de la matrice n'est pas nul.
Considérons le système d'équations linéaires à n inconnues:
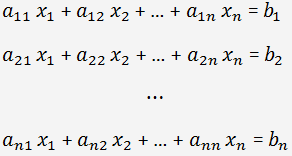
Matrice composée des coefficients de ce système est carrée.
Déterminant d'un système d'équations linéaires.
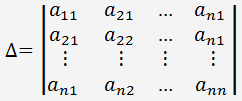
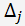
- est le déterminant de la matrice en remplaçant la jème colonne avec le membres de droite des équations du système
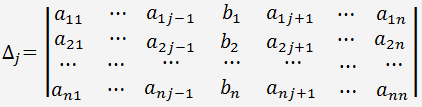
Si le déterminant d'un système n'est pas nulle
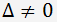
, alors le système est cohérent et a une solution unique.
La solution est donnée par par la règle de Cramer:
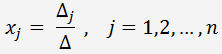
Résolution du système de trois équations linéaires par la règle de Cramer
Considérons un système de trois équations linéaires à trois inconnues
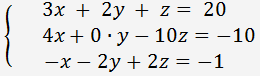
Calcul du déterminant du système de trois équations linéaires à trois inconnues:
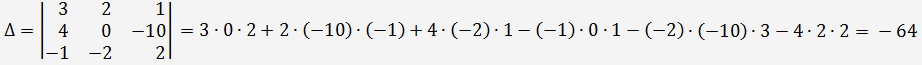
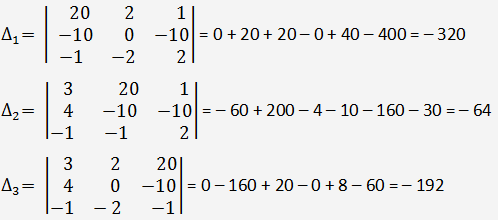
En règle de Cramer nous obtenons
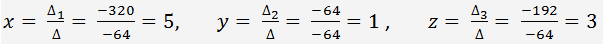
Résolution du système de trois équations linéaires par la méthode de Gauss
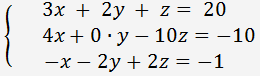
Divisez la première équation par 3
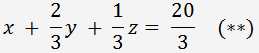
Multiplier l'équation (**) par 4 et ajouter les temps -1 à la deuxième équation, multiplier l'équation (**) par (-1) et soustraire de la troisième équation. Nous obtenons le système suivant
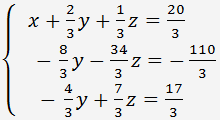
Diviser la deuxième équation par
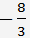
et obtenir
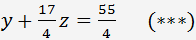
Multiplier l'équation (***) par
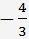
et soustraire de la troisième équation. En conséquence, nous obtenons le système d'équations suivant
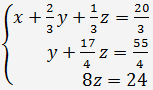
De de la dernière équation nous z=3. En substituant cette valeur dans la deuxième équation, nous obtenons:
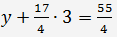
=> y=1
En substituant les valeurs de y et z dans la première équation, on trouve x
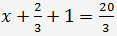
=> x=5
Les solutions de système sont donc: x=5, y=1, z=3
La calculatrice d'équations mémorise l'historique des calculs.

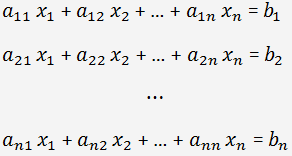
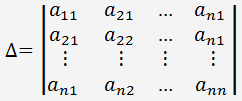
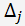 - est le déterminant de la matrice en remplaçant la jème colonne avec le membres de droite des équations du système
- est le déterminant de la matrice en remplaçant la jème colonne avec le membres de droite des équations du système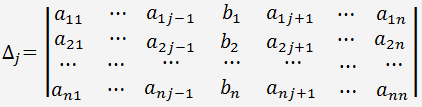
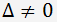 , alors le système est cohérent et a une solution unique.
, alors le système est cohérent et a une solution unique.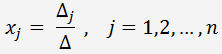
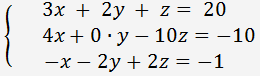
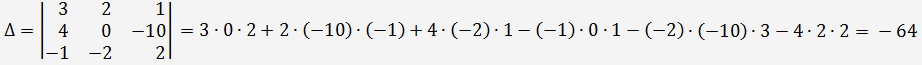
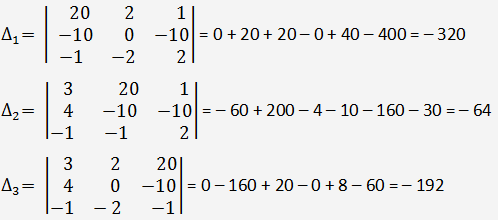
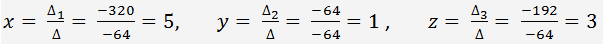
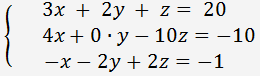
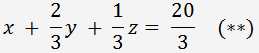
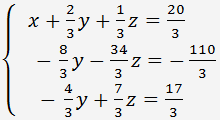
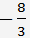 et obtenir
et obtenir 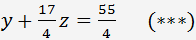
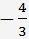 et soustraire de la troisième équation. En conséquence, nous obtenons le système d'équations suivant
et soustraire de la troisième équation. En conséquence, nous obtenons le système d'équations suivant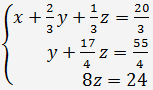
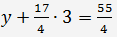 => y=1
=> y=1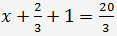 => x=5
=> x=5