Les équations du troisième degré
Une équation du troisième degré (équation de degré 3), ou équation cubique, est une équation de la forme
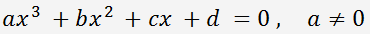
où
x est l'inconnue et
a,
b,
c et
c appelés coefficients de l'équation, avec
a différent de 0, sinon c'est du second degré.
Comment résoudre une équation du troisième degré
Format de équations prédéfinis pour résoudre des équations du troisième degré de la forme ax
3 + bx
2 + cx + d= 0. Pour résoudre une équation, entrer les coefficients 'a', 'b', 'c' et 'd' et cliquez sur Résoudre.
La calculatrice d'équations mémorise l'historique des calculs.
L'application calcule les racines d'une équation cubique (réelles et complexes) par la méthode de Cardan.
Résolution des équations du troisième degré : Méthode de Cardan
Considérons l'équation du troisième degré suivante:
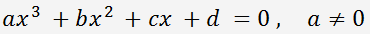
Diviser tous les termes par
a 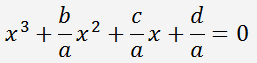
et posons x
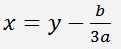
L'équation se ramène à une équation de la forme
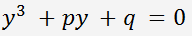
, où
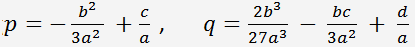
Le discriminant de l'équation cubique est
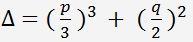
Par les formules de Cardan, les racines de l'équation du troisième degré:
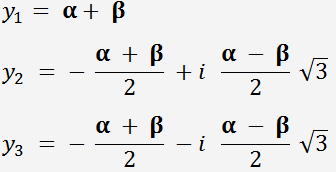
où
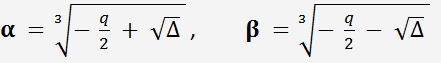
Pour chaque
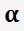
vous devez prendre
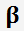
, pour lequel
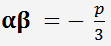
Si
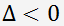
, l'équation admet trois racines réelles.
Si
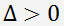
, alors une racine réelle et deux sont complexes conjugués.
Si
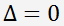
, l'équation admet deux racines réelles. Si p = q = 0, l'équation a une racine réelle.

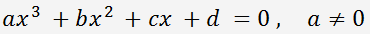
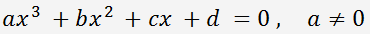
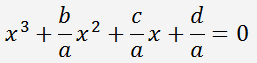
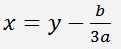
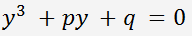 , où
, où 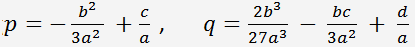
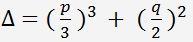
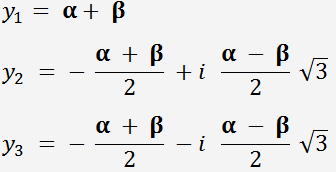
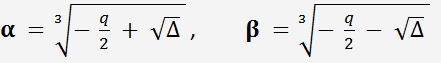
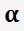 vous devez prendre
vous devez prendre 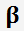 , pour lequel
, pour lequel 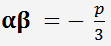
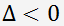 , l'équation admet trois racines réelles.
, l'équation admet trois racines réelles.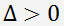 , alors une racine réelle et deux sont complexes conjugués.
, alors une racine réelle et deux sont complexes conjugués.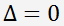 , l'équation admet deux racines réelles. Si p = q = 0, l'équation a une racine réelle.
, l'équation admet deux racines réelles. Si p = q = 0, l'équation a une racine réelle.