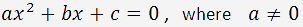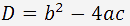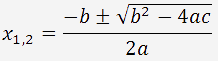Les équations du second degré
Une équation du second degré, ou équation du deuxième degré, ou équation quadratique, est une équation de la forme
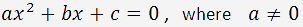
où
x est l'inconnue et
a,
b et
c appelés coefficients de l'équation, avec
a différent de 0, sinon c'est du premier degré.
Comment résoudre une équation du second degré à une inconnue
Pour résoudre une équation du second degré, entrer les coefficients
a,
b et
c et cliquez sur "Résoudre".
L'application calcule le discriminant et racines réelles et complexes.
Résoudre des équations du second degré
Commencer par calculer le discriminant.
Le discriminant de l'équation du second degré est
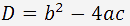
Le discriminant peut être positive, nulle ou négative. En fonction de la valeur de discriminant, il existe trois possibilités.
Trouver les racines des équations du second degré
Si le discriminant est positif (D > 0), l'équation admet deux solutions réelles.
Les racines d'une équation du second degré calculées par la formule:
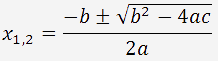
Si le discriminant est nul (D = 0), l'équation admet une racine réelle
Si le discriminant est négatif (D < 0), alors l'équation n'a pas de racines réelles - l'équation a deux racines complexes.